eu, christian ubiratan.

Durante a “era dos dados”, entender os conceitos básicos de criptografia é essencial para não ficar perdido quanto à proteção e ao uso das suas informações. Começando assim, pode parecer que esse tema é novo, mas, na verdade, a história da criptografia começa há muitos anos (cerca de 4.000 anos atrás), passando por tensões e inovações nas Guerras Mundiais e em diversas outras histórias de espionagem, até chegar na criptografia moderna.

Nesse texto veremos:

• Objetivos da criptografia;
• Provas de conhecimento-zero (zero-knowledge proof);
• História da criptografia (antiga).

Objetivos da criptografia

Do grego: kryptós (escondido) + gráphein (escrita), a criptografia estuda as formas de estabelecer uma comunicação segura (A quer se comunicar com B sem que C consiga entender a mensagem). Assim, os seus objetivos são diversos, incluindo:

• Garantir a confidencialidade, integridade e autenticidade de informações;
• Estabelecer comunicações mais seguras;
• Criação de dinheiro digital (anônimo e seguro);
• Criar protocolos seguros (para eleições, leilões, transações e outras modalidades).

Entre diversos outros objetivos que necessitam da segurança da informação para serem executados. Um exemplo interessante (e particularmente intrigante) são as provas de conhecimento-zero. Imagine que você deseja provar para outra pessoa que conseguiu resolver algum problema, sem de fato revelar a solução. Seria isso possível? É justamente sobre isso que tratam as provas de conhecimento-zero. Acompanhe o tópico abaixo para entender melhor esse conceito.

Provas de conhecimento-zero (zero-knowledge proof)

Imagine que um professor propôs a sua turma um desafio: encontrar o Wally em uma página do Where’s Wally. Você fala para um amigo que conseguiu realizar tal feito, mas ele, cético por não ter sido capaz de achar, não acredita. Como você poderia provar para ele que realmente achou o Wally, sem revelar a sua localização? Tente pensar um pouco antes de continuar lendo. Uma das possíveis maneiras seria recortar um pequeno buraco (do tamanho do Wally) em um grande pedaço de papelão, em seguida pedir para o seu amigo se virar enquanto você coloca o Wally aparecendo no furo. Ao se virar, o seu amigo não deve conseguir reconhecer a posição do Wally na folha (pois o papelão está cobrindo-a), mas agora sabe que você, com efeito, encontrou o Wally. Esse exemplo é ilustrativo para mostrar o quão poderoso pode ser o conceito das provas de conhecimento-zero (mas não é uma prova ou demonstração rigorosa).

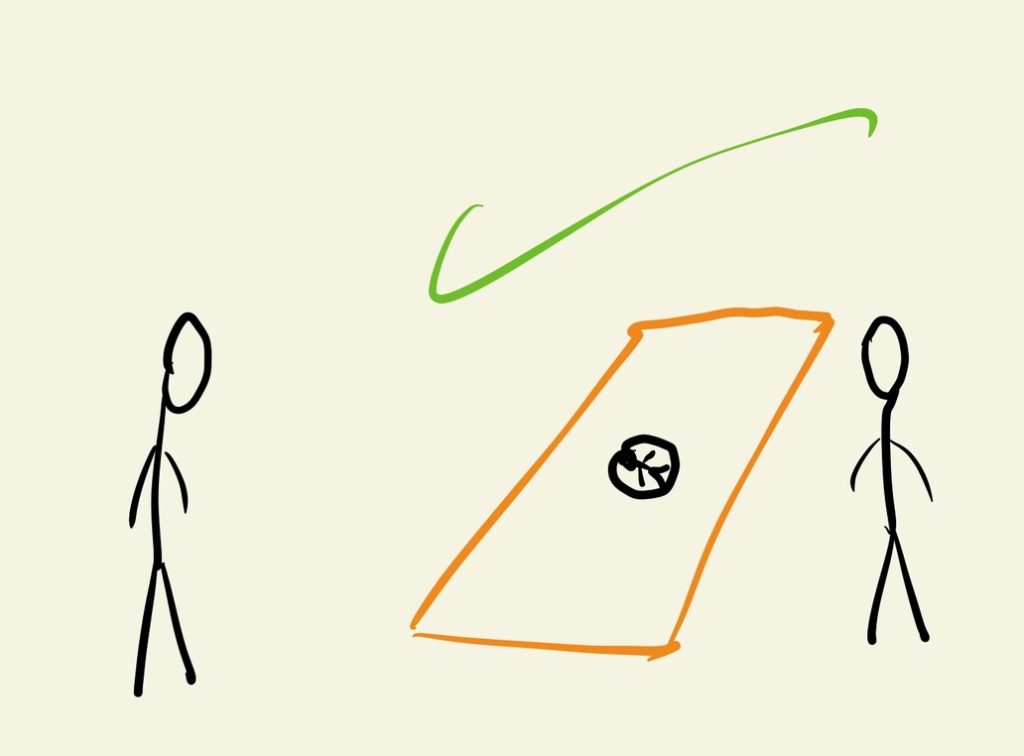
Em outros casos, a prova é feita através de alguns testes, que vão garantindo com maior probabilidade que há conhecimento sobre o fato tal qual se aumenta a quantidade de testes. Segue mais um exemplo, publicado pela primeira vez por Jean-Jacques Quisquater e outros autores no artigo: “How to Explain Zero-Knowledge Protocols to Your Children”. Imagine agora que Peggy quer provar para Victor que descobriu a palavra secreta necessária para abrir uma porta mágica em uma caverna. A caverna tem um formato de um anel, com dois caminhos que se encontram na porta mágica (então ambos caminhos podem funcionar tanto como entrada, quanto como saída).

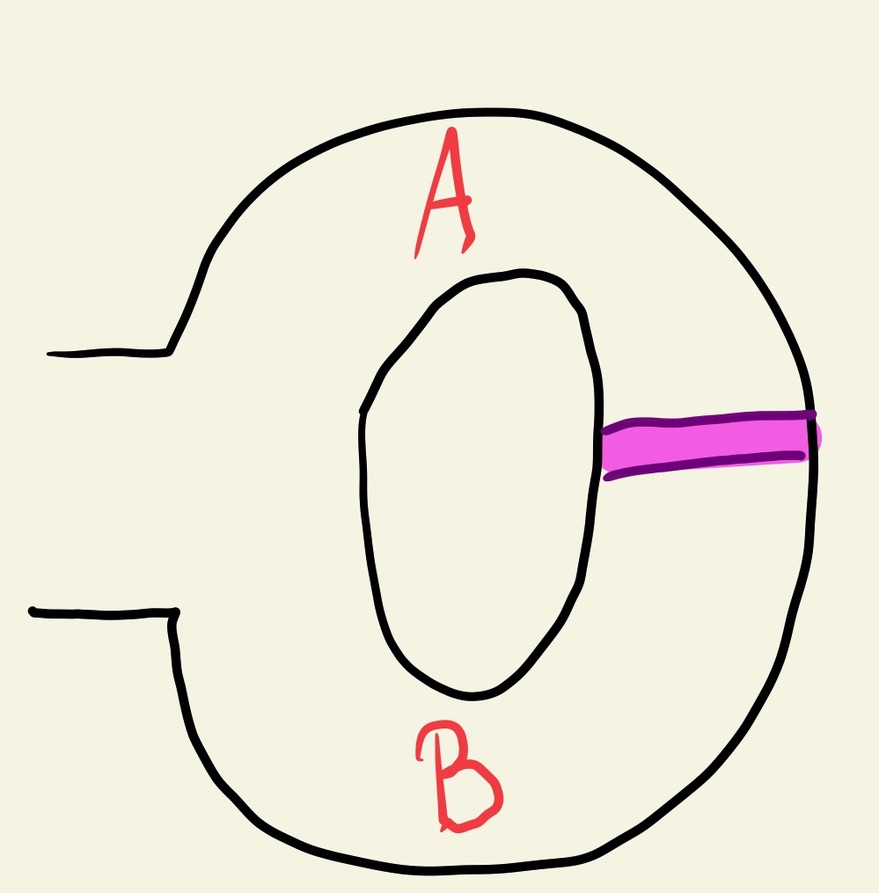
Victor quer saber se Peggy conhece a palavra secreta, mas ela, apesar de desejar provar que a conhece, não quer revelá-la. Nesse caso, como eles poderiam proceder (novamente, tente resolver antes de continuar lendo)? Há uma reposta inicial simples baseada nesses requisitos: os dois podem ir juntos para a entrada da caverna, e Victor observa Peggy entrar por A e sair por B (então ele teria certeza de que ela sabe a palavra secreta mesmo sem saber qual é).

Muito fácil? Vamos então adicionar mais um desafio: Peggy não deseja revelar para mais ninguém (exceto Victor) que ela sabe a palavra secreta (ou seja, apenas Victor deve ganhar o conhecimento de que ela sabe, no final da prova). Agora, a nossa primeira prova não é mais eficaz, pois ela poderia ser observada por outras pessoas, ou registrada por Victor, de modo a provar convincentemente para o mundo que ela conhece a palavra secreta. Como resolver esse novo problema?

Eis uma solução: primeiro eles rotulam os caminhos da caverna como A e B. Em seguida, Victor espera do lado de fora da caverna enquanto Peggy entra e vai por um dos caminhos A ou B (sem que Victor saiba qual caminho ela escolheu). Então, Victor entra na caverna e grita por qual dos caminhos ela deve retornar (uma escolha que ele deve ter feito ao acaso). Se ele gritar o caminho pelo qual ela entrou, então basta que ela retorne por ele. Já no caso em que ele gritar a porta oposta (ela entrou por A e ele gritou para ela voltar por B, ou vice-versa) seria necessário que ela abrisse a porta mágica para ir ao encontro dele pelo caminho correto. Visto que Victor escolheria A ou B aleatoriamente, haveria uma chance de 50% de Peggy não precisar abrir a porta. Assim, quanto mais vezes o experimento fosse realizado, mais improvável seria a hipótese de que Peggy estaria escolhendo sempre os mesmos caminhos de Victor (com 20 repetições as chances já seriam apenas 1/1.048.576, cerca de um em um milhão).

Com isso, Victor poderia ter convicção de que Peggy de fato conhece a palavra secreta, mas ele não seria capaz de revelar isso para o mundo. Ainda que ele gravasse o experimento, alguém assistindo à gravação não seria convencido de que ela não é alguma artimanha ou falsificação, a única coisa que pode ser mostrada é Victor gritando um caminho e Peggy aparecendo nele (o que, diferente da nossa primeira solução, pode facilmente ser uma manipulação em que ambos estabeleceram os caminhos de antemão).

Em momentos (simples) como estes é que eu me lembro da frase do Arthur C. Clarke:

“Qualquer tecnologia suficientemente avançada é indistinguível da magia“

Arthur C. Clarke

As provas de conhecimento-zero, e a maioria dos assuntos que eu abordo ou vou abordar nesse blog, podem não ser muito avançadas ou sequer serem uma tecnologia, mas, ainda assim, ao estudá-los são todos indistinguíveis da magia.

História da criptografia

Como foi dito na introdução, a criptografia existe desde tempos remotos. Assim, vamos entender um panorama da sua evolução, começando pelas cifras de substituição, como a famosa e simples cifra de César, até um alcançar um breve entendimento de como a computação mudou a história.

Primeiro devemos entender o que são as cifras. Podemos defini-las por:

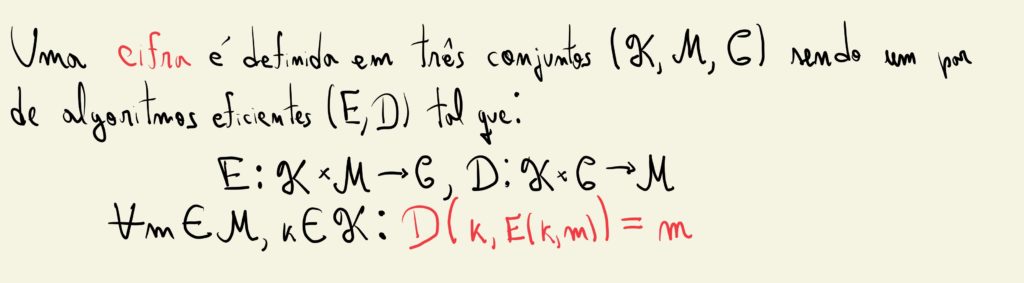
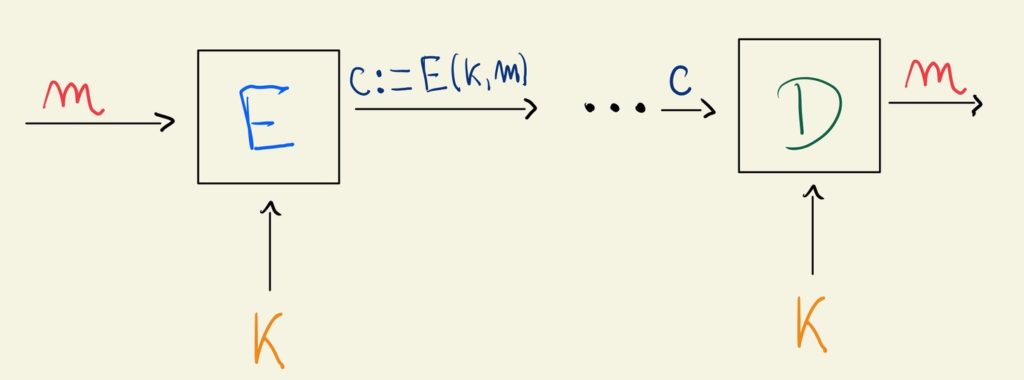
Explicando melhor: dada uma chave k, do conjunto K, devemos conseguir encriptar uma mensagem m, do conjunto M, através de um algoritmo E, tal que E(k, m) resulta em um texto cifrado, e devemos conseguir também decifrar a mensagem m com um algoritmo D, tal que D[k, E(k, m)] = m, ou seja, o algoritmo D, quando utilizado com a chave correta, transforma um texto encriptado na mensagem original.

Entendido a definição formal do nosso objeto de estudo, vamos para a história. Vale lembrar que os exemplos dados aqui tratam sobre criptografia com chaves simétricas, ou seja, tanto quem envia a mensagem, quanto quem recebe, devem possuir a mesma chave (que deve permanecer secreta para o mundo). Há outra forma de criptografia mais moderna, que iremos abordar futuramente, a qual a criptografia é assimétrica.

— Cifras de chaves simétricas

• Cifras de substituição

Nas cifras de substituição, como sugere o nome, cada item (letras ou bits, por exemplo) é substituído por outro item. Então, conhecendo a chave que foi utilizada para cifrar o texto, basta realizar a operação inversa para transformar o texto cifrado na mensagem original. Apesar de ser muito utilizada como veremos abaixo (no governo da Roma Antiga, na Primeira Guerra Mundial e até pela máfia italiana), essa categoria de criptografia quando mal utilizada, pode ser facilmente “quebrada”.

Apesar do grande número de chaves possíveis (cada letra pode se tornar qualquer uma das 26, incluindo permanecendo ela mesma) na maioria dos casos práticos em que são utilizadas é fácil decifrar cifras de substituição. Para se ter uma noção da quantidade das chaves que se pode formar, basta notar que cada letra pode se transformar em qualquer outra, mas duas letras não podem ser encriptada na mesma letra (se A virar F e B também virar F, não seria possível descriptografar a mensagem). Portanto, há 26•25•24…•2•1 = 26! ≈ 2⁸⁸ possibilidades, aproximadamente a quantidade de átomos no corpo humano.

No entanto, esse tipo de cifra, como veremos posteriormente, está sujeito a ataques utilizando simplesmente o texto cifrado (em alguns casos é possível descobrir a mensagem apenas analisando o texto encriptado). Isso pode ser feito através da análise da frequência das letras, por exemplo (afinal, a letra A costuma aparecer bem mais do que o W ou o Y).

— Cifra de César

Uma das formas mais simples das cifras de substituição são as cifras de César. Recebe esse nome em homenagem ao próprio Júlio César que utilizava a cifra com 3 trocas para proteger segredos militares. O seu mecanismo pode ser feito por um algoritmo em que a cada letra do alfabeto é designado um número, por exemplo, A = 1, B = 2, …, Z = 26, e para encriptar o texto basta somar alguma constante ao número de cada letra para obter o texto cifrado (somando 3, no nosso exemplo, A => D, B => E, …, Z => C).

Como pode-se perceber, não há uma chave propriamente dita, mas os valores são transformados dados uma constante. Por isso, a cifra de César é extremamente fácil de decifrar, já que só existem 26 possibilidades distintas para o valor de mudança, então, dado um texto cifrado qualquer, basta testar as 25 opções (não precisamos testar o próprio texto cifrado) e escolher a que faz sentido. Mesmo assim, ainda em 2006, a polícia foi capaz de prender um chefe da máfia italiana após decifrar as mensagens de bilhetes que utilizavam uma cifra similar à cifra de César.

Decifrando uma cifra de César

Vamos supor que nós sabemos que a mensagem abaixo foi um texto encriptado pela cifra de César:

CANV MJB XWIN

Para tentarmos decodificá-la, basta irmos testando as possíveis opções de “rotação” até encontrar o texto significativo (que muitas vezes possui inclusive um contexto conhecido, como uma localização ou horário para ataque). Então, vamos testar!

Poderíamos facilmente fazer os 25 testes manualmente, mas para trazer um pouco mais de emoção para o desafio, que tal tentar programar um código que teste as possibilidades?

Segue uma demonstração do código em Python abaixo (para estudar ou testar o código, basta ir para o Google Colab e clicar no botão “Play” da célula):

https://colab.research.google.com/drive/1N6Yb1iZvBcF1g5WE2nfD-08lwquUAC8g?usp=sharing

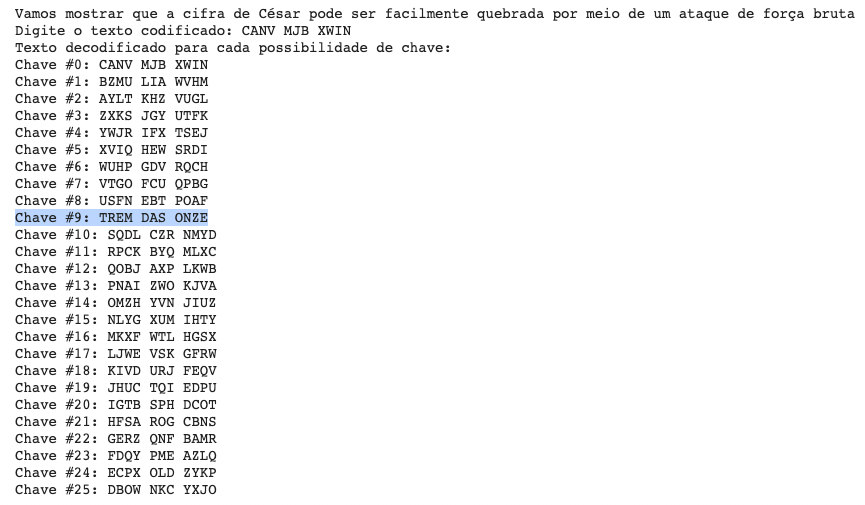
Como podemos ver, a única opção que faz sentido em português é a “Chave #9”, por isso, podemos afirmar que a nossa mensagem inicial é “TREM DAS ONZE”.

Um desafio adicional para quem se interessou e quer tentar resolver a cifra sozinho, seja com um programa, seja à mão (essa agora está sem os espaços entre as palavras):

JVIVJFCMVLVJJRDREURLDWFXLVKVEFZEJKR

— Cifra de Vigenère

Avançando bastante no tempo, agora no século XVI, o italiano Giovan Battista Bellaso melhorou a cifra de César (o nome Vigenère se dá por uma atribuição errônea da invenção da cifra para Blaise de Vigenère). Apesar de que, pelos motivos já citados, ela pode muitas vezes ser decifrada pelo texto cifrado, chegou a ser utilizada pelos Estados Confederados da América, na Guerra Civil Americana, e durante a Primeira Guerra Mundial.

O seu funcionamento é o seguinte: primeiro se escolhe uma chave para criptografar a mensagem, depois basta copiá-la em cima da mensagem (repetindo-a quantas vezes for necessário). Para criptografar a mensagem, basta fazer a adição módulo 26 (soma, divide por 26 e obtém o resto) do valor de cada letra da mensagem (normalmente A = 0, B = 1, …, Z = 25) com o valor de cada letra da chave.

Segue abaixo um exemplo do processo para encriptar a frase “LA VEM A ONDA” (sem os espaços) utilizando a chave “MAR”:

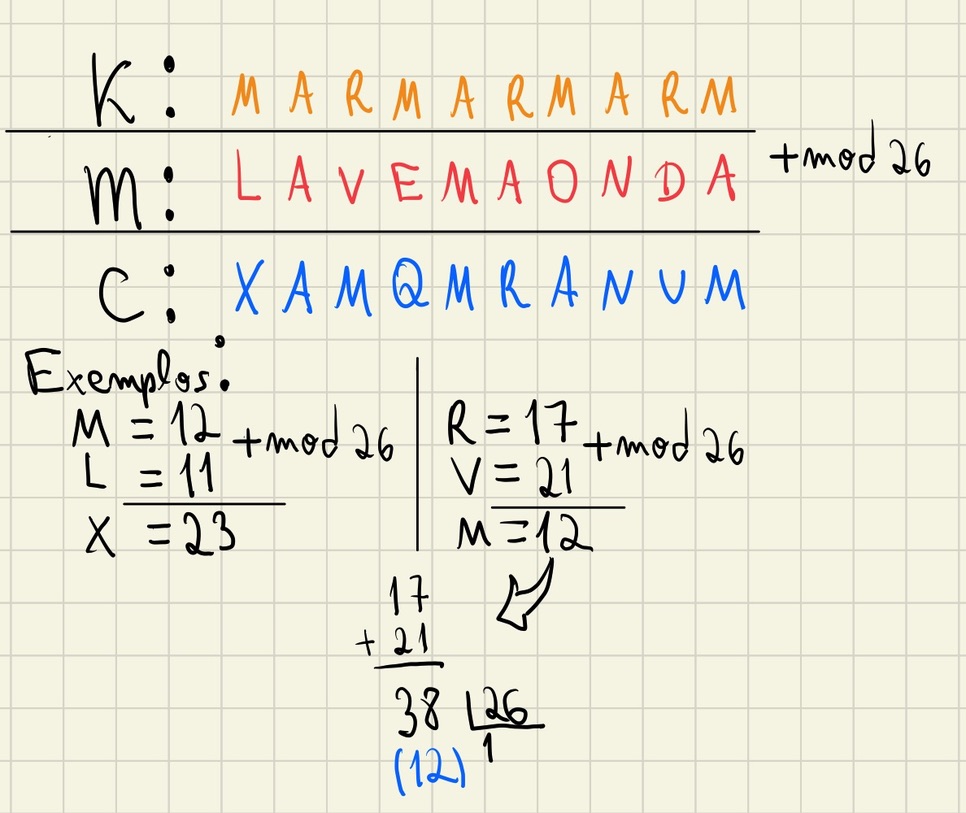
— Máquina de rotores

Como último exemplo de cifra de substituição, temos as máquinas de rotores. Criada por volta de 1870, e muito utilizada até a Segunda Guerra Mundial, ela se baseia em sucessivas tabelas de substituição.

Essa categoria de criptografia ficou bastante famosa com o filme de 2015 “O Jogo da Imitação”, que retrata o uso desse sistema por meio da máquina alemã Enigma. Com uma combinação de sistemas mecânicos e elétricos, a máquina alcançava um poder criptográfico muito maior que suas antecessoras (porém, como bem demonstrado no filme, ainda é suscetível a ataques a partir do texto interceptado).

Cada rotor acrescentado traz consigo uma 26 novas posições, então com 4 rotores (sem considerar configurações adicionais que eram utilizadas para melhorar a tecnologia), teríamos 26•26•26•26 = 26⁴ posições possíveis.

Segue abaixo um exemplo ilustrativo de uma máquina de rotor simples (lembrando que máquinas como a Enigma possuem um funcionamento bem mais complexo, aumentando consideravelmente a quantidade de posições possíveis):

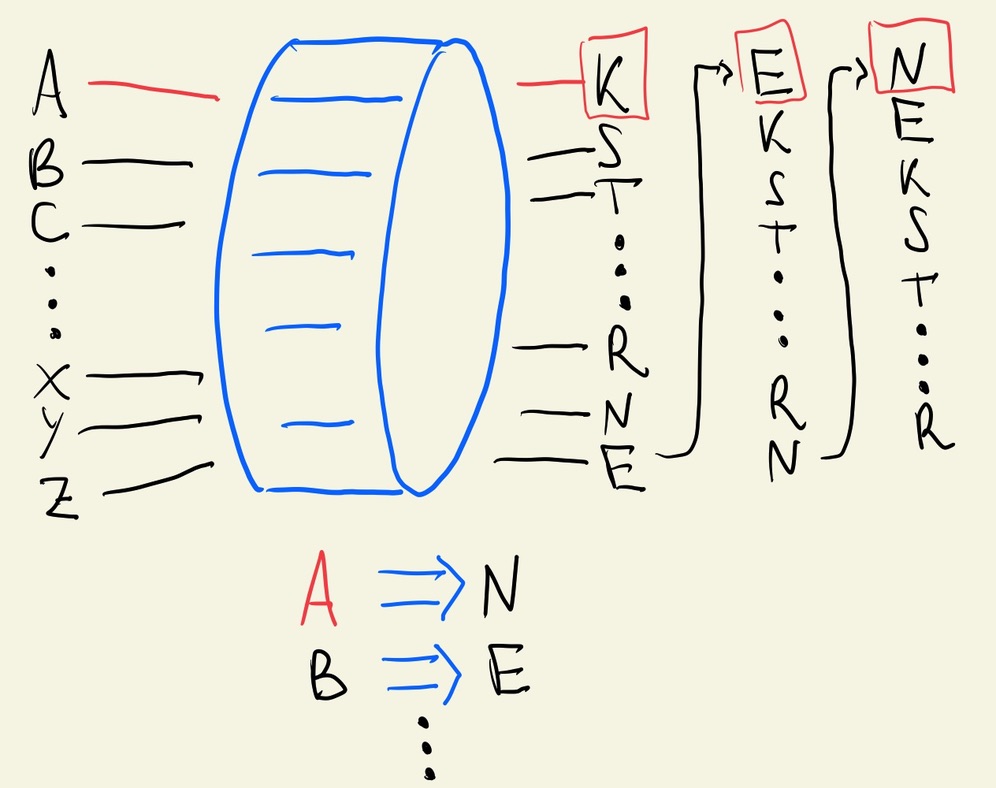
Como esse texto já se encontra bastante extenso, iremos continuar com a história da criptografia (a parte moderna, em que entra em jogo a computação) no texto seguinte.